DATA ANALYSIS PACKAGE SYMBOL

MonteCarloSimulation

MonteCarloSimulation[expr,i,{param1distribution1,param2distribution2,...}] carries out a Monte Carlo simulation with i iterations, to propagate uncertainties (in NDV objects or standard Mathematica Distribution objects) in expr. Parameters in expr may be separately specified as rules paramidistributioni, where distributioni can be either an NDV object or a standard Mathematica distribution object.

DetailsDetails

  • MonteCarloSimulation uses random sampling from the input parameter distributions to estimate the distribution of the output variable, resulting uncertainties, and other parameters useful for sensitify analyses.
  • MonteCarloSimulation uses the RandomVariate function to generate random samples.
  • MonteCarloSimulation can be run in parallel, making use of the ParallelEvaluate function.
  • MonteCarloSimulation returns a symbolic MonteCarloResult object, which can be used to access various parameters from result["property"].
  • MonteCarloSimulation does not have the attribute HoldFirst, so Hold should be applied to the expression where necessary.
  • MCEvaluate or MCE can be used if only the basic information in form of a DV object is required.
  • DVEvaluate can be used if only the basic uncertainty propagation is required and the expressions is relatively linear. As this is using analytical expressions, this is much faster.
  • Parameters with uncertainties can be included directly into the expression, or they can be defined in the third argument and referenced in the expression.
  • Apart from NDV objects, all standard Mathematica distributions such as PoissonDistribution can be used to specifiy input parameter uncertainties.
  • The following options can be given:
  • UseParallelKernelsFalsespecifies whether parallel kernels should be used for the simulation.
    MatchPattern_specifies that only function results matching this pattern should be used.
    MissingBehaviorAutomaticspecifies how expressions with head Missing should be interpreted in the context of other functions.
  • Properties that can be accessed include:
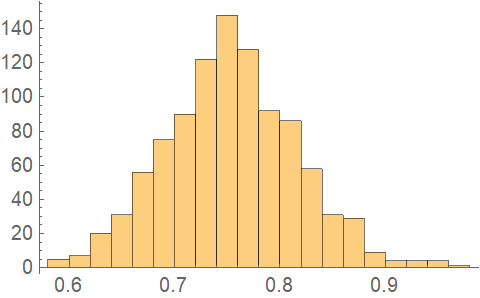
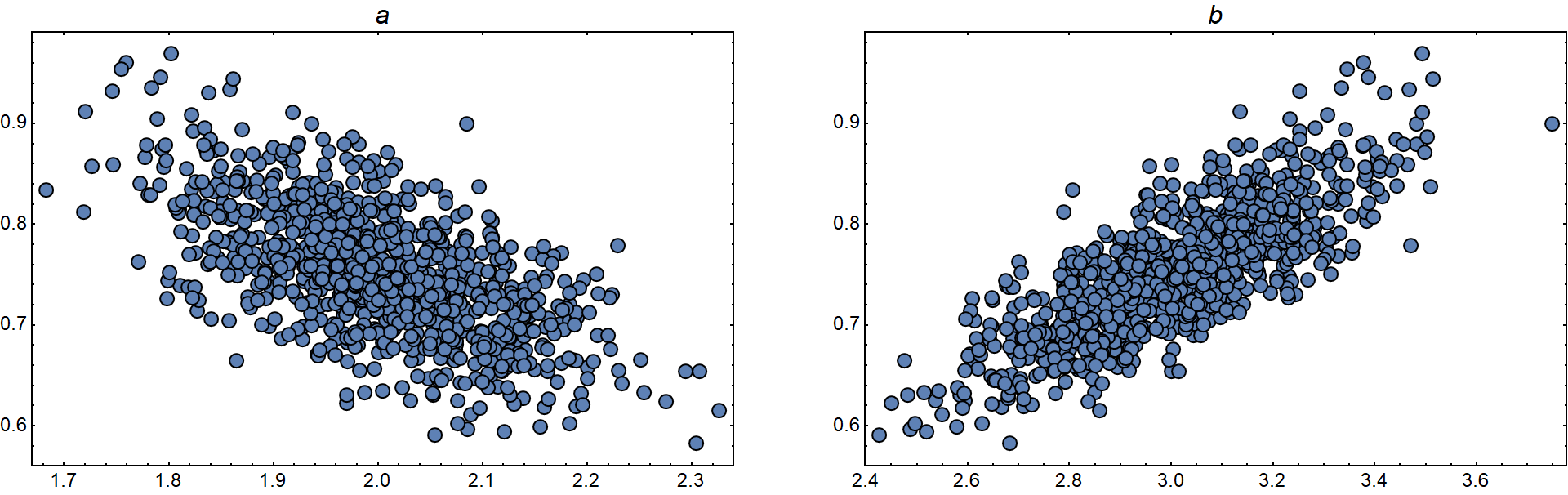
  • "SingleMean"Expression as evaluated using the means of the input parameters
    "SingleMeanDV"DV object including the confidence intervals.
    "SingleMeanNDV"NDV object based on the calculated standard deviation.
    "QuantileCI"Confidence intervals, calculated from quantiles.
    "DistributionMean"Mean of all random expression evaluations
    "DistributionMeanDV"As "SingleMeanDV" but using the DistributionMean
    "DistributionMeanNDV"As "SingleMeanNDV" but using the DistributionMean
    "FindDistribution"FindDistribution for output
    "EmpiricalDistribution"EmpiricalDistribution for output
    "StandardDeviation"StandardDeviation of output sample
    "Histogram"Histogram plot of output sample
    "SensitivityPlots"Plots of the randomly sampled input parameter values vs. the resulting output value
    "SimulationData"Raw random sampling/output data
  • Some properties work only properly if the expression is numeric if evaluated, but most of them (e.g. "SingleMeanDV", "QuantileDV", "Histogram", ...) thread over lists and associations.
  • Some properties use the confidence level set by SetConfidenceLevel.

ExamplesExamplesopen allclose all

Basic Examples  (1)Basic Examples  (1)

Carry out a simple Monte Carlo Simulation for a numeric function with two input parameters with uncertainties and 1000 iterations:

In[1]:=
Click for copyable input
Out[1]=

Get a NDV object for the resulting output:

In[2]:=
Click for copyable input
Out[2]=
In[3]:=
Click for copyable input
Out[3]=

Show a histogram of the output:

In[4]:=
Click for copyable input
Out[4]=

Show sensitivity plots (scroll to right for second plot):

In[5]:=
Click for copyable input
Out[5]=

Get some more properties:

In[6]:=
Click for copyable input
Out[6]=
In[7]:=
Click for copyable input
Out[7]=

Scope  (1)Scope  (1)

Options  (1)Options  (1)

Top